|
|
By Jo Nova
As Western grids are teetering, people are suddenly realizing demand for electricity is about to skyrocket
Unstoppable demands are about to meet immovable rocks. A year ago the grid managers thought they had their five year plans figured out, but now the same experts think we are going to need to add twice as much generation as they did then. The watt-hogs have arrived to chew on some gigawatt hours.
The usual slow grid planning processes are getting upended. Take the US State of Georgia for example. They have scored lots of new electric vehicle and battery factories, a few large “clean energy” manufacturing projects, and have attracted a bunch of energy-sucking data centers, but all of these things add massive loads to the grid.
In the last 22 years demand for electricity hasn’t growth much, so in 2022 Georgia Power were expecting to close their coal fired plants pretty soon, and not even put forward a new plan til 2025. Instead Georgia Power are knocking on the state regulators door to let it expand generation. They’re now expecting winter demand will grow 17 times faster than their previous plan, and summer use will explode to 28 times more*. In 2022 they thought the system might be OK until 2030. Now they think the “shortfalls” start by 2025. And 70% of the capacity they want to add is fossil fuel based.
It could be the worst possible time, say, for politicians to force cars and trucks to run off the grid too…
The Editorial Board, The Wall Street Journal
Artificial-intelligence data centers and climate rules are pushing the power grid to what could become a breaking point.
AEP Ohio says new data centers and Intel’s $20 billion planned chip plant will increase strain on the grid. Chip factories and data centers can consume 100 times more power than a typical industrial business. … A new Micron chip factory in upstate New York is expected to require as much power by the 2040s as the states of New Hampshire and Vermont combined.
Electricity demand to power data centers is projected to increase by 13% to 15% compounded annually through 2030.
The shortage of power is already slowing the building of new data centres by up to six years. It’s so bad, Amazon just bought a 1,200 acre data warehouse right next to a nuclear plant so it can live off nuclear energy. The data center may use up to 960 MW of power, which would be nearly 40% of all the power provided by the nuclear plant.
It’s almost like the CCP is in charge of our electricity grids?
The green subsidies make the unreliable generators happy, but more unreliables in turn destroys the market for the reliable guys. There’s not much point running major capital infrastructure as a back up for a second rate generators. Not surprisingly, many of the essential generators are about to go off to grid-heaven forever and the new replacements are, as the bureaucrats say “not clearly identified” yet.
PJM Interconnection runs the wholesale power market on 13 US States. They latest report signals trouble coming according to the WSJ:
About 20 gigawatts of fossil-fuel power are scheduled to retire over the next two years—enough to power 15 million homes—including a large natural-gas plant in Massachusetts that serves as a crucial source of electricity in cold snaps. PJM’s external market monitor last week warned that up to 30% of the region’s installed capacity is at risk of retiring by 2030.
Meantime, the Inflation Reduction Act’s huge renewable subsidies make it harder for fossil-fuel and nuclear plants to compete in wholesale power markets. The cost of producing power from solar and wind is roughly the same as from natural gas. But IRA tax credits can offset up to 50% of the cost of renewable operators.
All the artificial intelligence arriving appears to be shining a light onto human stupidity.
Who could have guessed that if we subsidize unreliable generators we would get an unreliable grid?
______________________________
*If you follow that link, beware, the Atlanta Journal-Constitution article was supported by a partnership with Green South Foundation and Journalism Funding Partners. See at ajc.com/donate/climate/.
10 out of 10 based on 105 ratings
9.1 out of 10 based on 14 ratings
By Jo Nova
Sometime a few years ago the Carbonistas stopped trying to pretend it was science, climate change has morphed into a ecclesiastical piñata instead. (If they whack it hard enough, grants fall out).
Instead of talking about 30 year trends (because they were wrong), the experts started coloring weather maps blood red and hyperventilating with every warm weekend. So it makes perfect sense they need the ritual reminders of holy mythology, and this is one of those stories. It’s the weekly nod for the awestruck fanatics that the world really does revolve around “climate change”. They can nod solemnly, and pat each others solar panels.
The theory is that because our showers are too long or our beef steaks are too big (don’t you feel important?), the poles are melting and some ice near the poles has dribbled out to the equator, slowing the planet’s spin. Since the Earth is a rotating ball of rock 10,000 kilometers across, the movements of a few millimeters of water on the surface are somewhat minor. But nevermind. So the dire news, such as it isn’t, is that the Earth’s clocks might have to be wound back by one whole second in 2026.
Someone will do a cost-benefit analysis soon on whether spending a quadrillion dollars can prevent this.
The drama here is that this is something has never been done before, at least since clocks were invented, five minutes ago in Earth’s geological history. The ice has, of course come and gone many times all of its own accord, and clocks have leapt forward one second 27 times since the 1970s, but this is the epochal moment that you can tell your grandchildren about — the day the Earth started slowing, and you were there! (Nobody mention that dinosaurs only had 23 hours in a day, no wonder they went extinct. Let’s obsess about a second, instead!)
In a not-so-great moment in modern science communication the BBC manages to say everything and nothing all at once:
Accelerating melt from Greenland and Antarctica is adding extra water to the world’s seas, redistributing mass.
That is very slightly slowing the Earth’s rotation. But the planet is still spinning faster than it used to.
The effect is that global timekeepers may need to subtract a second from our clocks later than would otherwise have been the case.
Got that? So climate change is delaying the great negative leap second. Wait?
And it’s unprecedented, of course:
“Things are happening that are unprecedented.” The negative leap second has never been used before and, according to the study, its use “will pose an unprecedented problem” for computer systems across the world.
The world may have adjusted its day-length 100,000 times, but this is the first time a sentient species with optical strontium clocks and a Windows 11 quagmire will try to go back in time by one second.
“This has never happened before, and poses a major challenge to making sure that all parts of the global timing infrastructure show the same time,” Mr Agnew, who is a researcher at the University of California, San Diego told AFP news agency.
It’s like Y2K all over again but with sermons and hymns.
When all the world is a climate-change-grant, everything on Earth is climate change problem.
REFERENCE (for those wondering if this is an April 1 trick)
Duncan Carr Agnew (2024) A global timekeeping problem postponed by global warming, Nature, 4334. https://doi.org/10.1038/s41586-024-07170-0
9.9 out of 10 based on 94 ratings
8.6 out of 10 based on 18 ratings
By Jo Nova
There are so many holes in the Holy Carbonista Bible it’s easy to find one to surprise a BBC interviewer with.
Now that Guyana has discovered the joys of major oil deposits, the President came prepared. But because the BBC is so robotically predictable, Irfaan Ali knew exactly what they would ask, but host Stephen Sackur, seemingly had no idea what was coming. If only the BBC had interviewed a few skeptics in the last thirty years…
…
“Let me stop you right there,” he said. “Did you know that Guyana has a forest that is the size of England and Scotland combined, a forest that stores 19.5 gigatons of carbon, a forest that we have kept alive?”
“I’m going to lecture you on climate change. Because we have kept this forest alive that you enjoy that the world enjoys, that you don’t pay us for, that you don’t value.
“Guess what? We have the lowest deforestation rate in the world. And guess what? Even with the greatest exploration of oil and gas we will still be net zero.”
— The Telegraph
9.9 out of 10 based on 120 ratings
Celebrate Easter with Joy
9.1 out of 10 based on 31 ratings
9 out of 10 based on 16 ratings
By Jo Nova
That which must not be spoken
Every news outlet today is saying how good it is that “relations” with China have thawed, like it was just a bad patch of weather, and now the clouds have cleared they’ve allowed us to sell them wine again. But there is a kind of collective amnesia about why relations froze in the first place.
Just to recap, through incompetence or “otherwise” naughty-citizen China leaked a likely lab experiment, lied about it, and destroyed the evidence. They stopped it spreading at home but sent it on planes to infect the rest of the world. Then when Scott Morrison, Australian Prime Minister, dared ask for an investigation in April 2020, within a week China threatened boycotts, and followed up with severe anti-dumping duties on Australian barley. After which the CCP discovered “inconsistencies in labelling” on Australian beef imports, and added bans or tariffs on Australian wine, wheat, wool, sugar, copper, lobsters, timber and grapes. Then they told their importers not to bring in Australian coal, cotton or LNG either. The only industry they didn’t attack was iron ore, probably because they couldn’t get it anywhere else. In toto, the punishment destroyed about $20 billion dollars in trade, and everyone, even CNN, knew this was political retribution and a message to the world.
As Jeffrey Wilson, Foreign Policy, described it in November 2021
“… its massive onslaught against Australia was like nothing before. Whereas China usually sanctions minor products as a warning shot—Norwegian salmon, Taiwanese pineapples—Australia was the first country to be subjected to an economywide assault.”
But perhaps the communist party had nothing to hide?
Not to put a fine point on it, but on January 14th, 2020, China told the world they had “found no clear evidence of human-to-human transmission “. A Chinese CDC expert said “If no new patients appear in the next week, it might be over.” They didn’t mention that things were already so bad in Wuhan in December 2019, that even doctors one thousand kilometers away in Taiwan suspected it was spreading human to human. Taiwan demanded answers from the WHO on December 31. The next day, the CCP destroyed all the virus samples, information about them, and related papers. But perhaps it was just an innocent bat-pangolin thing, yeah?
So after four years of pain in order to stand bravely against the bully, what concessions, exactly, did our current leadership win? There’s no investigation, no answers, no apology, no nothing and no reason to think it won’t happen again.
In fact to smooth the wheels, Australia dropped the WTO cases against China for their bad behaviour with barley and wine. But the negotiation geniuses didn’t insist that China drop its WTO case against us (which was instigated two days after the Australian cases). And so it comes to pass that this week China won the WTO steel case against us.
* * *
Lest we forget:
Ten years ago China said it was worried about race based genetic bioweapons — Who, exactly, had a biotech war on their minds? In 2015 Chinese military scientists ominously predicted the Third World War would be fought with biological weapons. Meanwhile the Chinese military were helping out with the Wuhan viral research projects, and if one virus wasn’t enough, they still have another 1,640 other viruses to play with. The multicultural melting pot of stupid ideas is glowing like lava on all sides of the Pacific. The US Defence Department also sent money to the Wuhan lab to counter “Weapons of Mass Destruction” which apparently helped to create one. And the CSIRO, and Australian universities had worked with the Wuhan Virology Lab too (which they forgot to mention for 18 months?)
Meanwhile in related news in the last three years, the Biden family gained $31m in deals with high level CCP operatives. There’s a shadow war in space “every day”. And Net Zero remains a security threat, yet the West claps along.
Lions Photo by Serg Balak on Unsplash
9.8 out of 10 based on 124 ratings
Best wishes to everyone…
9.9 out of 10 based on 16 ratings
By Jo Nova
Our news is filled with fatuous lies every single day.
Mr Bowen, Minister for Changing the Weather, wants to force efficiency standards on Australian cars so we “have more choices”, he says. Mysteriously, it seems there are companies overseas making cheap, clean, wonderful cars who selfishly refuse to sell them to us. Crazy eh?
Would that be because:
- Car salesmen want to save the world?
- There’s no market for efficient cars here. Australians prefer cars that burn up and waste fuel!
- It costs more to sell to nations with no efficiency standards since they have to install the Fuel Worse-ifier?
Or could it be they know Australians won’t buy their damn cars unless the government bans the cheaper ones first?
Mr Bowen, now says they never had a target. Of course! And people are mobbing him in the street wanting to buy expensive European EV’s:
By Jess Malcolm, The Australian
Energy and Climate Change Minister Chris Bowen has walked away from Labor’s target to have 89 per cent of new car sales electric by 2030, casting doubt on the government’s green agenda.
“We don’t have a particular EV target,” Mr Bowen said on Wednesday morning.”
“We have a determination to give Australians more choices. So many Australians come up to me in the street and say, I’d like my next car to be an EV but I’m not really seeing the range of choices that are affordable.
“And they’re right because there are many more affordable EVs that are available in other countries that aren’t available here because we don’t have efficiency standards.”
It’s like he believes political rules create miles-per-gallon efficiency, not engineering.
Or perhaps he’s not serving the Australian people at all, but some entity somewhere has promised him a great job one day if he can help create a market for cars in Australia that hardly anyone would willingly buy if they weren’t forced to?
10 out of 10 based on 123 ratings
9.6 out of 10 based on 11 ratings
By Jo Nova
Imagine the outcry if a coal plant was obliterated by hail?
A few days ago, a 3,300 acre solar power plant in Texas suffered major hail damage. This was a plant so new it was still under construction. The Fighting Jays solar project started generating in 2022, but was not expected to be fully complete until the end of 2024. In theory it was supposed to last for 35 years.
It is so large they boasted that it covers 2,499 football fields (like that is a good thing). Despite the vast footprint, it was rated at only 350 MW. At noon at peak production it could generate about half of what one forty year old coal fired turbine makes all day every day, and every night too.
Collecting low density energy is more expensive than the wish-fairies might think.
At an average construction price of $1 million per megawatt the project likely cost about $350 million dollars. In order to rebuild it, they will need to remove and dispose of the broken panels, so it may cost even more.
The Fighting Jays solar farm was insured against hail damage. Presumably insurance premiums will be rising.
Locals are worried about the possibility of contamination with heavy metals, plastics and other chemicals in the local water supply. Hopefully they won’t leave it all there to rot.
On the plus side, the hailstorm reduced some pollution of the Texas energy market.
h/t Colin
10 out of 10 based on 119 ratings
10 out of 10 based on 8 ratings
By Jo Nova
The “Misinformation Industry” has been caught with its pants down — accidentally finding, then burying, the information that nearly everyone in their own industry “leans left”.
This is a field that generated headlines about how conservatives are more susceptible to believing misinformation, and conservatives consume more Facebook disinformation. It would be awkward then if the whole field turned out to be leftist academics, and they tried to hide that, which is exactly what just happened.
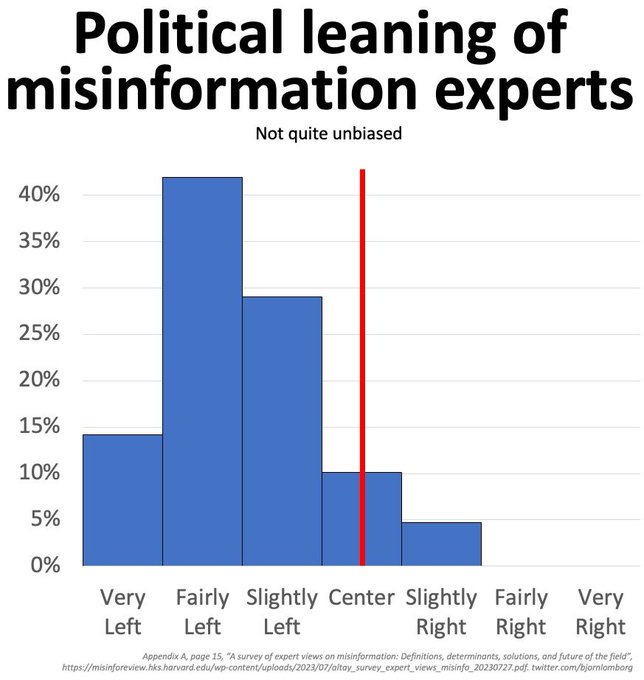
The leading “journal” on misinformation surveyed 150 of its own academic experts, then forgot to mention that one of the most striking and significant results from their own survey was that being a “Misinformation Expert” was a left wing phenomena.
 Bjorn Lomborg noticed the statistics on their self-admitted political leanings buried in an appendix, and graphed it himself. He writes: “Misinformation experts are perhaps not quite unbiased”.
There was barely a conservative among them:
Speaking of misinformation, it’s a little misleading, don’t you think, to pretend this doesn’t matter in a field “devoted” to researching political misinformation?
It seems The Misinformation Review has been misinforming its readers.
The Misinformation Industry looks, acts and smells like a leftist invention to censor the right
Looking at their own statistics, the “misinformation” experts are a self-confessed group of leftist soft-scientists with little understanding of maths, physics, mining, chemistry and real life.
Experts leaned strongly toward the left of the political spectrum: very right-wing (0), fairly right-wing (0), slightly right-of-center (7), center (15), slightly left-of-center (43), fairly left-wing (62), very left-wing (21).
And they specialize in media-science and political-science and think that’s a “broad range”:
The misinformation experts represent a broad range of scientific fields. Experts specialized in psychology (39), communication and media science (32), political science (22), computational social sciences (17), computer science (9), sociology (8), journalism (8), philosophy (5), other (4), medicine/other (2), linguistics (2), history (1), physics (1).
Experts of what exactly?
As a theoretical field of science, the experts of misinformation could not even agree on a definition of misinformation itself. Only one in ten thought misinformation was “false information” alone. The rest felt that “misleading people” intentionally, or even unintentionally could qualify, which means the misinformation label can apply to anyone discussing a fact which they thought was true, and is actually true, but (as defined by the left-voting-experts) was “misleading” in the wrong context.
They just want to shut you up
When asked what we should do about misinformation, the correct answer, of course, is “explain why it’s wrong”. But the experts didn’t even think of that — instead they suggest nine ways to hide information and the vast majority of the pool of “experts” were happy with nearly all of them — deplatform, silence, moderate and censor away!
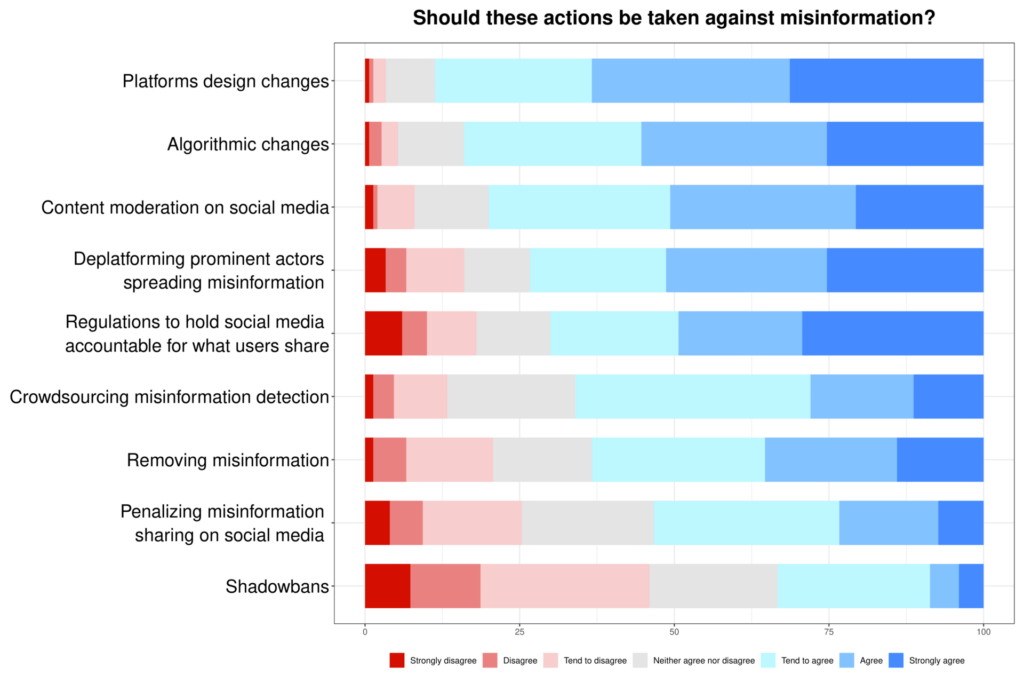
When asked “why do people believe misinformation?” the politically biased experts didn’t even blink — it was the human failures of confirmation bias, social identity and partisanship they declared — while buried six feet deep in confirmation bias, social identity and partisanship.
REFERENCE
Altay, S., Berriche, M., Heuer, H., Farkas, J., & Rathje, S. (2023). A survey of expert views on misinformation: Definitions, determinants, solutions, and future of the field. Harvard Kennedy School (HKS) Misinformation Review. https://doi.org/10.37016/mr-2020-119
Website: misinforeview.hks.harvard.edu
h/t Ryan Maue, David Maddison
9.9 out of 10 based on 101 ratings
10 out of 10 based on 7 ratings
By Jo Nova
Ponder how far we have come when more than half of the US sees the media, not just as self-serving, biased hacks, but as The Enemy itself.
“Fake News” is annoying, but active lies and suppression are a campaign to steal something from you — or everything: your money, your health, your vote and your children. There is no “town square” anymore, no common forum where ideas are batted back and forth until both sides agree. There is only entrenched polarization. A house divided, and no shared meals. Fomenting civil war.
Rasmussen Reports asked 1,114 likely US voters whether the media are “truly the enemy of the people”, and an amazing 60% agreed.
By Nicole Wells, NewsMax
According to the survey, of the 60% majority who agree with Trump’s 2019 assessment that the media are “the enemy of the people,” 30% strongly agree with the presumptive GOP presidential nominee; 36% disagree with the statement, including 21% who strongly disagree.
It’s much more widespread across the political spectrum than you might think:
On whether the media are “truly the enemy of the people,” 79% of Republicans, 60% of independents, and 41% of Democrats at least somewhat agree.
Even half of Democrat voters agree the media runs on Democrat talking points:
Broken down by political party, 78% of Republicans, 61% of independents, and half of Democrats say it is at least somewhat likely that the news media’s political coverage is driven by Biden campaign talking points.
Donald Trump not only talked about the Fake News Media, but called the media “the enemy of the people” from as far back as 2017.
Recently, he talked of a “bloodbath” in the auto industry, which was twisted into false claims he was calling for a political bloodbath if he loses. The Rasmussen poll showed that media bias still has power — 40% of US voters still believe the lie that he was talking about widespread political violence by his supporters. 49% knew the truth, and 11% were unsure. Voters younger than 40 were less likely to have figured out the truth.
But only 3% of Twitter users still believe the “Bloodbath hoax”.
Rather surprisingly, Rasmussen ran a similar poll in 2021 with similar results. The 60% are entrenched.
The Democrats, the Financial House media owners, and Deep State would have to be sweating. Control of the media has been a powerful weapon but that ship is breaking up on the rocks of reality. Another round of “Factcheckers” can’t save it now. All they have left is the USS Censor Ship.
Thought for the day: How do we reach more of the believer 40%?
UPDATE: At least one commenter still believes the media care about subscriptions
The profits from subscribers and advertising are trivial compared to the power that comes from controlling the narrative. Shareholder owners invest a small part of their portfolio in their media-empire so they can then hide their subsidies, pointless industries and crony deals from public outrage and scrutiny.
The uber billionaires can lose money on the media so the rest of their investment portfolio reaps in the dough from their power to control the narrative, influence elections, and suppress public dissent.
See: What if the media was just the lobbying agency for bigger profit making ventures?
9.9 out of 10 based on 97 ratings
8.4 out of 10 based on 10 ratings
9 out of 10 based on 9 ratings
By Jo Nova
Martin Durkin’s work will be studied one day like Thucydides as a record of a bizarre moment in human history. It is so quintessentially British. I thought I’d seen it all in the climate debate, but this is so well done, perfect for a curious, matter-of-fact mind. It pulls you along, with timeless nostalgic footage in a classic English delivery, calmly unravelling mythology. It will resonate with people who remember cities, cars and great documentaries of long ago.
Because it’s not angry or activist it’s a gift you can send to friends who are science nerds, or history buffs, or who remember the sixties. Send it to people with teenagers who have no idea the curriculum hides a half a billion years of history. Send it to green friends, who have no idea a third of the food made in Africa rots before it can be eaten without fossil fuels and plastic to preserve and transport it.
Imagine the effect if this was shown at schools.
It’s the story of how an activist movement became a big industry, they say. But I can’t help thinking it was a big industry that grew an activist movement…
Honest scientists are no longer free,
To discover; what science should be,
Fearing censure and sacking,
And from colleagues no backing,
With consensus are forced to agree.
–Ruairi
9.7 out of 10 based on 128 ratings
10 out of 10 based on 13 ratings
|
JoNova A science presenter, writer, speaker & former TV host; author of The Skeptic's Handbook (over 200,000 copies distributed & available in 15 languages).
Jo appreciates your support to help her keep doing what she does. This blog is funded by donations. Thanks!
Follow Jo's Tweets To report "lost" comments or defamatory and offensive remarks, email the moderators at: support AT joannenova.com.au
Statistics
The nerds have the numbers on precious metals investments on the ASX
|
The link on Bitchute: https://www.bitchute.com/video/ONMGnSiOLhjG/
and Vimeo https://vimeo.com/924719370
UPDATE: Surprisingly it is still on Youtube today (Sunday) and with subtitles in other languages. Vote it up there while you still can…